Функции распределения и функции распределения вероятностей. Дискретные и непрерывные случайные величины. Функция распределения
Каждая случайная величина полностью определяется своей функцией распределения.
Если ![]() — случайная величина, то функция
— случайная величина, то функция
![]()
называется функцией распределения случайной величины ![]() .
.
Здесь ![]() — вероятность того, что случайная величина
— вероятность того, что случайная величина ![]() принимает значения, не превосходящие числа x.
принимает значения, не превосходящие числа x.
Функция распределения любой случайной величины обладает следующими свойствами:
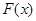 определена на всей числовой прямой
определена на всей числовой прямой 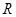 ;
;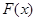 не убывает, т.е. если
не убывает, т.е. если 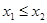 , то
, то 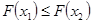 ;
;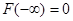 ,
, 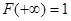 , т.е.
, т.е. 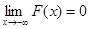 и
и 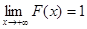 ;
;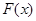 непрерывна справа, т.е.
непрерывна справа, т.е. 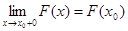 .
.
Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация об этой случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением. Так что, когда говорят о нормальном распределении, то подразумевают случайную величину, имеющую нормальную функцию распределения. В дальнейшем будем использовать термин распределение.
У дискретной случайной величины функция распределения ступенчатая.
Если ![]() — дискретная случайная величина, принимающая значения x1 <x2 < …< xi < …. с вероятностями p1 , p2 , …, pi , …. то таблица вида
— дискретная случайная величина, принимающая значения x1 <x2 < …< xi < …. с вероятностями p1 , p2 , …, pi , …. то таблица вида
xi |
x1 |
x2 |
… |
xi |
… |
pi |
p1 |
p2 |
… |
pi |
… |
называется распределением дискретной случайной величины.
Пример 1. Подбросим монету один раз. Будем полагать «выигрыш» равным единице, если монета упала цифрой вверх и нулю, если она упала вверх гербом.
Случайная величина — сумма «выигрыша.
Распределение суммы выигрыша:
xi |
0 |
1 |
pi |
0.5 |
0.5 |
Функция распределения случайной величины — суммы выигрыша:
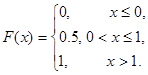
На рис.1 приведен график функции распределения. Построенный в Excel.
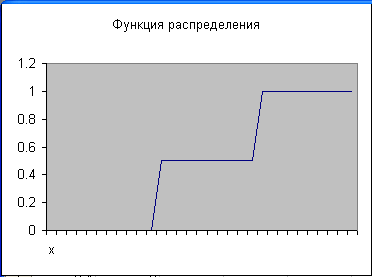
Пример 2. Бросаем один раз игральную кость. Случайное событие — кость упала одной из граней вверх. Случайная величина — число, выпавшее на верхней грани.
Распределение числа очков:
xi |
1 |
2 |
3 |
4 |
5 |
6 |
pi |
|
|
|
|
|
|
Функция распределения случайной величины — суммы выигрыша:
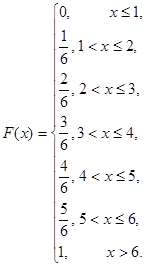
Пример 3. Бросаем один раз игральную кость. Случайное событие — кость упала одной из граней вверх. Если на верхней грани выпало меньше 3, полагаем «выигрыш» равным 0, если больше — 1, если выпало 3 очка — 2.
Распределение суммы выигрыша:
xi |
0 |
1 |
2 |
pi |
|
|
|
Функция распределения случайной величины — суммы выигрыша:
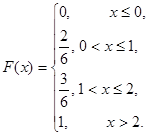
Пример 4. На отрезке [0, 1] наугад (случайно) поставлена точка. Измеряется расстояние точки от левого конца отрезка. Полагаем случайную величину равной расстоянию от точки до левого конца отрезка.
Функция распределения непрерывной случайной величины — расстояния случайной точки единичного отрезка до левого конца отрезка:
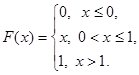
Пример 5. В урне красный, белый и чёрный шары. «Выигрыш» равен количеству белых шаров среди двух, выбранных наугад. Эта случайная величина дискретная, она принимает значения из дискретного множества {0, 1}.
Распределение суммы выигрыша:
xi |
0 |
1 |
pi |
|
|
Функция распределения случайной величины — суммы выигрыша:
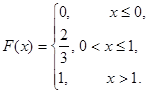
Пример 6. Банк планирует инвестировать свободные средства в один из двух фондов. Один из фондов имеет наибольшую доходность в период экономического подъёма, назовём его «Восход», другой — «Закат» — в период экономического спада. Оценивается доходность инвестиций для одного из трёх состояний экономики: подъём, стабильность, спад. Данные даны в таблице:
Состояние экономики |
Вероятность состояния |
Доходность (прибыль на каждые вложенные 1000 $) |
|
«Восход» |
«Закат» |
||
Спад |
0.2 |
– 100 |
+ 200 |
Стабильность |
0.5 |
+100 |
+50 |
Подъём |
0.3 |
+250 |
– 100 |
Случайная величина — доходность (средства вкладываются в тот фонд, который даёт наибольшую доходность).
Распределение доходности инвестиций:
xi |
100 |
200 |
250 |
pi |
0.5 |
0.2 |
0.3 |
Функция распределения случайной величины — суммы выигрыша:
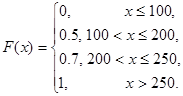
Если функция распределения ![]() непрерывна, то случайная величина
непрерывна, то случайная величина ![]() называется непрерывной случайной величиной.
называется непрерывной случайной величиной.
Плотность распределения вероятностей
Если функция распределения ![]() дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины
дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины ![]() , которая связана с функцией распределения
, которая связана с функцией распределения ![]() формулами
формулами
![]() и
и ![]() .
.
Отсюда, в частности, следует, что для любой случайной величины ![]() .
.
Вероятность того, что значение случайной величины ![]() попадает в интервал
попадает в интервал ![]() , вычисляется для непрерывной случайной величины по формулам:
, вычисляется для непрерывной случайной величины по формулам:
 или
или ![]() ,
,
а для дискретной случайной величины — по формуле:
![]() .
.