6. 2. Двухфакторный дисперсионный анализ
Пусть случайная величина ![]() зависит от двух признаков (факторов)
зависит от двух признаков (факторов) ![]() и
и ![]() .
.
Обозначим ![]() ,
, ![]() ,
, ![]() ,
, ![]() — уровни факторов
— уровни факторов ![]() и
и ![]() , соответственно.
, соответственно.
Результаты измерения случайной величины ![]() представлены в таблице
представлены в таблице
|
1 |
2 |
3 |
... |
|
1 |
|
|
|
... |
|
2 |
|
|
|
... |
|
... |
... |
... |
... |
... |
... |
|
|
|
|
... |
|
В каждой клетке таблицы – при каждом сочетании уровней факторов проведено по одному наблюдению (измерению). Тогда общее число наблюдений ![]() .
.
Обозначим через ![]() математическое ожидание
математическое ожидание ![]() при уровне
при уровне ![]() ,
, ![]() ; через
; через ![]() — математическое ожидание
— математическое ожидание ![]() при уровне
при уровне ![]() ,
, ![]() .
.
Если при изменении фактора ![]() сохраняется равенство
сохраняется равенство ![]() , то естественно считать, что величина
, то естественно считать, что величина ![]() не зависит от фактора
не зависит от фактора ![]() , принимается нулевая гипотеза
, принимается нулевая гипотеза ![]() . В противном случае,
. В противном случае, ![]() зависит от фактора
зависит от фактора ![]() .
.
Аналогично определяется зависимость от фактора ![]() , нулевая гипотеза
, нулевая гипотеза ![]()
При решении задачи будем предполагать, что выполняются следующие условия:
наблюдения при различных сочетаниях уровней факторов независимы и
при всех сочетаниях уровней факторов случайная величина ![]() нормально распределена с одной и той же дисперсией
нормально распределена с одной и той же дисперсией ![]() .
.
Изменчивость наблюдаемых факторов при переходе от одной клетки таблицы к другой может быть обусловлена как изменением уровней факторов, так и случайными неконтролируемыми факторами.
Изменчивость, вызванная случайными неконтролируемыми факторами, называется остаточной.
Вычислим общую среднюю результатов измерений по формуле
![]() .
.
Эту величину можно представить в другой форме, использующей групповые средние ![]() и
и ![]() :
:
![]() ,
, ![]() .
.
Точка в индексе величины ![]() означает, что суммирование ведется по i-й строке, а точка в индексе величины
означает, что суммирование ведется по i-й строке, а точка в индексе величины ![]() означает, что суммирование ведется по j-му столбцу.
означает, что суммирование ведется по j-му столбцу.
В этих обозначениях средняя результатов измерений вычисляется по формуле
![]() или
или ![]() .
.
Средняя изменчивость, вызванная фактором ![]() , вычисляется по формуле
, вычисляется по формуле
![]() .
.
Аналогично для изменчивости, вызванной фактором ![]() :
:
![]() .
.
Для характеристики изменчивости, обусловленной случайными факторами, вычисляем
![]() .
.
Общую изменчивость величины ![]() характеризуют величиной
характеризуют величиной
![]() .
.
Доказано, что ![]() .
.
Проверка гипотезы ![]() основывается на сравнении величин
основывается на сравнении величин ![]() и
и ![]() .
.
Если гипотеза ![]() верна, то величина
верна, то величина 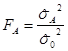 имеет распределение Фишера со степенями свободы
имеет распределение Фишера со степенями свободы ![]() и
и ![]() .
.
Зададимся уровнем значимости ![]() и найдем правостороннюю критическую точку
и найдем правостороннюю критическую точку ![]() — решение уравнения
— решение уравнения ![]() .
.
Если значение ![]() , вычисленное по результатам измерений удовлетворяет неравенству
, вычисленное по результатам измерений удовлетворяет неравенству ![]() , то гипотеза
, то гипотеза ![]() принимается.
принимается.
В противном случае – отвергается и можно заключить, что изменение фактора ![]() влияет на изменение величины
влияет на изменение величины ![]() .
.
Мерой этого влияния является коэффициент детерминации 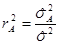 , который показывает, какая доля общей изменчивости величины
, который показывает, какая доля общей изменчивости величины ![]() обусловлена увеличением фактора
обусловлена увеличением фактора ![]() .
.
Аналогично проверяется гипотеза ![]() основывается на сравнении величин
основывается на сравнении величин ![]() и
и ![]() .
.
Если гипотеза ![]() верна, то величина
верна, то величина 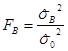 имеет распределение Фишера со степенями свободы
имеет распределение Фишера со степенями свободы ![]() и
и ![]() .
.
При уровне значимости ![]() правосторонняя критическая точка
правосторонняя критическая точка ![]() — решение уравнения
— решение уравнения ![]() .
.
Если значение ![]() , вычисленное по результатам измерений удовлетворяет неравенству
, вычисленное по результатам измерений удовлетворяет неравенству ![]() ,
,
то гипотеза ![]() принимается.
принимается.
В противном случае гипотеза ![]() отвергается и можно заключить, что изменение фактора
отвергается и можно заключить, что изменение фактора ![]() влияет на изменение величины
влияет на изменение величины ![]() .
.
Мерой этого влияния является коэффициент детерминации 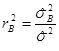 , который показывает, какая доля общей изменчивости величины
, который показывает, какая доля общей изменчивости величины ![]() обусловлена увеличением фактора
обусловлена увеличением фактора ![]() .
.
В рамках двухфакторного дисперсионного анализа можно получить более конкретное представление о случайной величине ![]() .
.
Ее модель на ![]() -м уровне фактора A и на j-м уровне фактора B имеет вид
-м уровне фактора A и на j-м уровне фактора B имеет вид
![]() ,
, ![]() ,
, ![]() ,
,
Где a — генеральное среднее случайной величины ![]() ,
,
![]() — слагаемое, которое описывает эффект влияния фактора A на случайную величину
— слагаемое, которое описывает эффект влияния фактора A на случайную величину ![]() на i-м уровне фактора A,
на i-м уровне фактора A,
![]() — слагаемое, которое описывает эффект влияния фактора B на случайную величину
— слагаемое, которое описывает эффект влияния фактора B на случайную величину ![]() на j-м уровне фактора B,
на j-м уровне фактора B,
![]() — слагаемое, которое описывает эффект влияния случайных факторов.
— слагаемое, которое описывает эффект влияния случайных факторов.
Величины ![]() — независимые случайные величины, имеющие одинаковое нормальное распределение
— независимые случайные величины, имеющие одинаковое нормальное распределение ![]() .
.
Если гипотезы ![]() и
и ![]() не отвергаются, то в рассмотренной модели параметры
не отвергаются, то в рассмотренной модели параметры
![]() и
и ![]() .
.
Величина ![]() является оценкой параметра
является оценкой параметра ![]() , а величина
, а величина ![]() — несмещенная оценка параметра
— несмещенная оценка параметра ![]() .
.
Если гипотезы ![]() и
и ![]() отвергаются, то: оценка параметра a равна
отвергаются, то: оценка параметра a равна ![]() , оценка параметра
, оценка параметра ![]() равна
равна ![]() , оценка параметра
, оценка параметра ![]() равна
равна ![]() ,
,
а величина ![]() служит несмещенной оценкой параметра
служит несмещенной оценкой параметра ![]() .
.
Пример
Проведите двухфакторный дисперсионный анализ таблицы. Запишите уточнённую модель.
|
|
|
|
|
|
10.9 |
11.1 |
9.9 |
11.51 |
|
13.3 |
15.2 |
14.8 |
14.9 |
|
17.3 |
18.0 |
19.6 |
19.3 |
На приведенном ниже рисунке изображён фрагмент листа Excel c результатами вычислений.
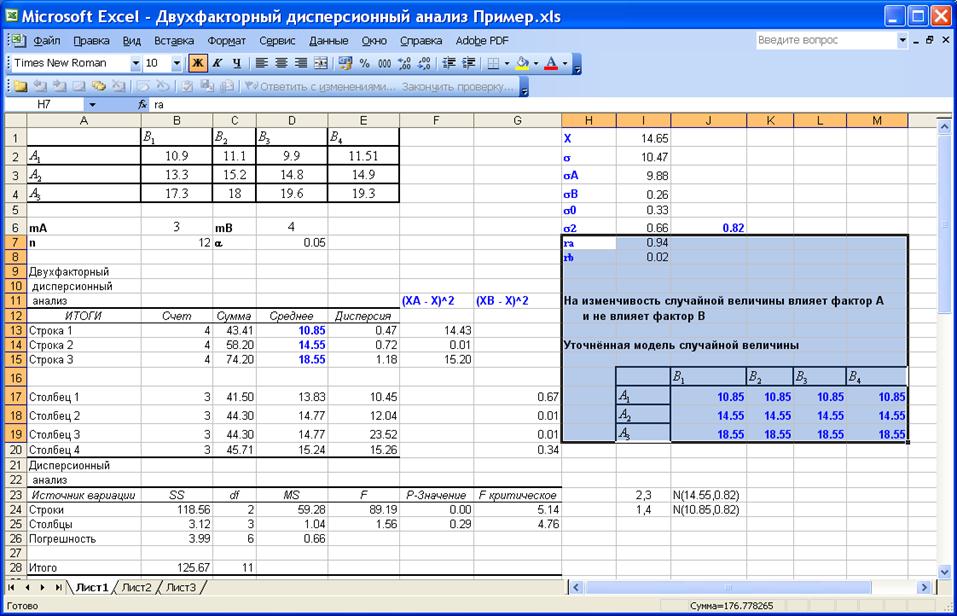
Выборочное значение критерия Фишера для фактора А попадает в критическую область, 89.19 > 5.14.
Фактор А является причиной изменчивости случайной величины.
Коэффициент детерминации для фактора А равен rA=0.94. Это означает, что более 94% всей изменчивости исследуемой случайной величины обусловлено изменением фактора А.
Выборочное значение критерия Фишера для фактора В не попадает в критическую область, 1.56 < 4.76.
Фактор В не является причиной изменчивости случайной величины.
На долю фактора В приходится только 2% изменчивости, поскольку rВ=0.02.
Для всех уровней фактора случайные величины распределены нормально со стандартным отклонением 0.82 и математическими ожиданиями 10.852, 14.55 и 18.55 соответственно для каждого уровня фактора.
Матрица, описывающая влияние факторов на изучаемое явление – уточнённая матрица.
Так, например, на уровнях А2 и В3 случайная величина имеет нормальное распределение ![]() .
.